Sobre el azar

Como buen psicólogo argentino, la obra del psicoanalista francés Jacques Lacan (1901-1981) no me es indiferente. En el intento de estudiar su Seminario número 11, me topé con la referencia a los conceptos aristotélicos de tyche y automaton, que pueden traducirse por azar y espontaneidad respectivamente. Para tratar de entender mejor esos conceptos fui al texto de Aristóteles ('Física'), pero lo cierto es que luego de leerlo me encontré más perdido que antes. Se me ocurrió entonces buscar en la web alguna página que pudiese ayudarme. En esa búsqueda encontré un artículo que no hablaba para nada de Aristóteles o Lacan, pero sí del azar, la teoría del caos, y su relación con la filosofía del matemático y lógico estadounidense Charles Peirce (1839-1914). Puesto sobre la pista del caos, recordé un librito que tenía en mi biblioteca, Las leyes del caos, escrito por uno de los padres del estudio de los procesos irreversibles, Ilya Prigogine (1917-2003), químico de origen ruso, premio Nobel en 1977. En este librito que no es para nada técnico, pues está escrito para que lo entendamos los legos, creí encontrar expresada de alguna manera la idea de que el caos es en el universo más numeroso que el orden. Quizá pueda leerse en este pasaje:

"Popper tiene una hermosa expresión, habla de relojes y nubes. La física clásica se interesaba ante todo por los relojes, la física actual más bien por las nubes (...) Podemos admirar la sencillez del movimiento planetario, la precisión asociada a los relojes, pero también podemos reconocer su carácter particular, casi único"

Acaso podamos hablar entonces de leyes precisas sólo de manera acotada, en un universo con pocos relojes y mayormente repleto de nubes. Esto me sugirió una imagen que quisiera comentar.

Se sabe que los griegos antiguos renegaban de los números irracionales, tanto que la Escuela Pitagórica decidió ocultar su existencia cuando fueron descubiertos, y peor aún, el pobre infeliz que traicionó el secreto fue expulsado de la secta y ejecutado. Los números adorados por los pitagóricos eran los naturales (1,2,3,4...), más los negativos (...-4,-3,-2,-1), más las fracciones (es decir, todos los cocientes de las divisiones entre aquellos números), conjunto al que se llama de "números racionales". Los números irracionales, aquellos que cuentan con una parte decimal de infinitas cifras no periódicas (como por ejemplo el número π 3,14159265..., que continúa hasta el infinito sin repetir sus cifras periódicamente) y que no pueden expresarse como cociente de ninguna división, arruinaban para los seguidores de Pitágoras la doctrina del número como ente perfecto que gobernaba el universo. Los griegos no iniciados en este secreto y que, por lo tanto, sólo conocían la existencia de los números racionales, creían entonces que éstos alcanzaban para cubrir todos los puntos de una recta. En otras palabras, pensaban que si representáramos cada número racional con un punto y pusiéramos cada punto uno al lado del otro, se obtendría una recta continua, sin agujeros. Entre el 0 y el 1 una infinidad de fracciones, entre el 1 y el 2 otra infinidad de fracciones, y así, hacia un lado y hacia otro de la recta.
He aquí la recta de los números racionales tal como la concebían los griegos antiguos, que desconocían la existencia de los números irracionales.

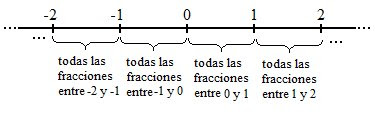Para ellos la recta estaba completa. Pero si consideramos la existencia de los números irracionales, entonces sabemos que esa recta de números racionales no es continua, algunos puntos faltan. Por ejemplo, en el lugar en el que debiera estar π no habrá nada más que un agujero.
Pero eso no es todo, puesto que la moderna teoría de conjuntos del matemático de origen ruso-alemán George Cantor (1845-1918) indica que el conjunto de los números irracionales es mayor que el de los números racionales. Cantor hizo complejísimos estudios sobre el infinito, resultando de su teoría la idea de que existen infinitos más grandes que otros. Si bien tanto el conjunto de números racionales como el conjunto de números irracionales tienen infinitos elementos, el segundo tiene infinitamente más elementos que el primero. Existen más números irracionales que racionales, ¡de modo que la recta de los griegos antiguos tiene más agujeros que puntos!
Resumiendo, allí donde los griegos antiguos creían ver una recta perfectamente continua de racionalidad, había en verdad casi un completo vacío irracional.

Volviendo al problema del caos, el azar, el orden, y la ley en el universo, adviértase que miramos hacia el mundo como si estuviera repleto de ley y necesidad. Invito al lector a que mire a su alrededor e intente detectar agujeros en donde falte la ley y todo suceda de manera caótica. Muy por el contrario, seguramente encontrará que las cosas están en su lugar: las sillas están donde deben estar; no se derriten, no se vuelan, no se desintegran. Las paredes, por su parte, son también totalmente previsibles. Obsérvese el monitor, cuyas leyes de funcionamiento quizá no conozcamos en absoluto. Esto no obsta para que sintamos firmemente que todo en él está en orden. El sentimiento de que nada queda por fuera del gobierno de alguna ley es casi continuo. Casi ninguna porción del mundo aparece como ajena, o por fuera del comercio con el resto de las cosas. Y sin embargo, quizá adolecemos de la misma ilusión que los griegos antiguos respecto de los números irracionales. Quizá el espectáculo del mundo que se nos aparece como continuo, lleno, sin saltos, sin ninguna de sus partes rota, sea en realidad una minúscula miríada de puntos sobre una infinidad de caos. Un leve desfasaje en la pulsación sobre la que percibimos el mundo nos enfrentaría sin velos con el azar, con un océano de acontecimientos sin ley.
Al decir de Lacan, podemos confiar sin embargo que mientras la ley del deseo marche sin problemas, el agujero quedará mayormente velado.